Ka Expression For Acetic Acid
16.4: Acid Strength and the Acid Dissociation Constant (Ka)
- Folio ID
- 47028
- To know the human relationship between acrid or base strength and the magnitude of \(K_a\), \(K_b\), \(pK_a\), and \(pK_b\).
- To understand the leveling upshot.
The magnitude of the equilibrium abiding for an ionization reaction tin can be used to determine the relative strengths of acids and bases. For instance, the general equation for the ionization of a weak acid in water, where HA is the parent acrid and A− is its conjugate base, is as follows:
\[HA_{(aq)}+H_2O_{(fifty)} \rightleftharpoons H_3O^+_{(aq)}+A^−_{(aq)} \label{16.5.ane} \]
The equilibrium constant for this dissociation is as follows:
\[Grand=\dfrac{[H_3O^+][A^−]}{[H_2O][HA]} \label{16.5.2} \]
As we noted earlier, because water is the solvent, it has an activity equal to 1, and then the \([H_2O]\) term in Equation \(\ref{16.v.2}\) is actually the \(\textit{a}_{H_2O}\), which is equal to 1.
Over again, for simplicity, \(H_3O^+\) can be written every bit \(H^+\) in Equation \(\ref{xvi.5.3}\).
\[HA_{(aq)} \rightleftharpoons H^+_{(aq)}+A^−_{(aq)} \characterization{16.5.iii} \]
Keep in listen, though, that free \(H^+\) does non be in aqueous solutions and that a proton is transferred to \(H_2O\) in all acid ionization reactions to form hydronium ions, \(H_3O^+\). The larger the \(K_a\), the stronger the acid and the higher the \(H^+\) concentration at equilibrium. Like all equilibrium constants, acid–base ionization constants are actually measured in terms of the activities of \(H^+\) or \(OH^−\), thus making them unitless. The values of \(K_a\) for a number of common acids are given in Table \(\PageIndex{i}\).
| Acid | \(HA\) | \(K_a\) | \(pK_a\) | \(A^−\) | \(K_b\) | \(pK_b\) |
|---|---|---|---|---|---|---|
| *The number in parentheses indicates the ionization stride referred to for a polyprotic acid. | ||||||
| hydroiodic acid | \(HI\) | \(2 \times x^{9}\) | −ix.iii | \(I^−\) | \(5.5 \times x^{−24}\) | 23.26 |
| sulfuric acid (one)* | \(H_2SO_4\) | \(1 \times 10^{2}\) | −2.0 | \(HSO_4^−\) | \(1 \times ten^{−xvi}\) | xvi.0 |
| nitric acid | \(HNO_3\) | \(2.3 \times x^{1}\) | −1.37 | \(NO_3^−\) | \(4.iii \times ten^{−16}\) | xv.37 |
| hydronium ion | \(H_3O^+\) | \(i.0\) | 0.00 | \(H_2O\) | \(i.0 \times 10^{−14}\) | xiv.00 |
| sulfuric acid (2)* | \(HSO_4^−\) | \(1.0 \times 10^{−2}\) | 1.99 | \(SO_4^{2−}\) | \(nine.8 \times 10^{−xiii}\) | 12.01 |
| hydrofluoric acid | \(HF\) | \(6.iii \times 10^{−4}\) | 3.twenty | \(F^−\) | \(1.vi \times 10^{−11}\) | 10.80 |
| nitrous acid | \(HNO_2\) | \(5.vi \times 10^{−iv}\) | iii.25 | \(NO2^−\) | \(ane.8 \times 10^{−11}\) | 10.75 |
| formic acrid | \(HCO_2H\) | \(ane.78 \times ten^{−4}\) | three.750 | \(HCO_2−\) | \(5.six \times 10^{−eleven}\) | x.25 |
| benzoic acid | \(C_6H_5CO_2H\) | \(6.3 \times 10^{−5}\) | 4.20 | \(C_6H_5CO_2^−\) | \(1.vi \times x^{−10}\) | nine.eighty |
| acetic acrid | \(CH_3CO_2H\) | \(1.vii \times 10^{−five}\) | four.76 | \(CH_3CO_2^−\) | \(v.8 \times x^{−10}\) | 9.24 |
| pyridinium ion | \(C_5H_5NH^+\) | \(5.ix \times 10^{−6}\) | 5.23 | \(C_5H_5N\) | \(ane.seven \times 10^{−9}\) | 8.77 |
| hypochlorous acid | \(HOCl\) | \(4.0 \times 10^{−eight}\) | vii.40 | \(OCl^−\) | \(2.5 \times x^{−7}\) | half-dozen.lx |
| hydrocyanic acrid | \(HCN\) | \(6.2 \times 10^{−10}\) | ix.21 | \(CN^−\) | \(1.vi \times 10^{−5}\) | 4.79 |
| ammonium ion | \(NH_4^+\) | \(5.6 \times 10^{−10}\) | 9.25 | \(NH_3\) | \(1.eight \times x^{−5}\) | four.75 |
| water | \(H_2O\) | \(1.0 \times 10^{−14}\) | 14.00 | \(OH^−\) | \(1.00\) | 0.00 |
| acetylene | \(C_2H_2\) | \(i \times ten^{−26}\) | 26.0 | \(HC_2^−\) | \(1 \times 10^{12}\) | −12.0 |
| ammonia | \(NH_3\) | \(ane \times x^{−35}\) | 35.0 | \(NH_2^−\) | \(one \times ten^{21}\) | −21.0 |
Weak bases react with water to produce the hydroxide ion, as shown in the following general equation, where B is the parent base and BH+ is its conjugate acid:
\[B_{(aq)}+H_2O_{(l)} \rightleftharpoons BH^+_{(aq)}+OH^−_{(aq)} \label{16.5.4} \]
The equilibrium constant for this reaction is the base ionization constant (Thoub), besides called the base of operations dissociation abiding:
\[K_b= \frac{[BH^+][OH^−]}{[B]} \characterization{16.v.5} \]
Once once more, the activity of water has a value of 1, then water does not appear in the equilibrium constant expression. The larger the \(K_b\), the stronger the base and the college the \(OH^−\) concentration at equilibrium. The values of \(K_b\) for a number of common weak bases are given in Table \(\PageIndex{two}\).
| Base | \(B\) | \(K_b\) | \(pK_b\) | \(BH^+\) | \(K_a\) | \(pK_a\) |
|---|---|---|---|---|---|---|
| *Equally in Table \(\PageIndex{1}\). | ||||||
| hydroxide ion | \(OH^−\) | \(1.0\) | 0.00* | \(H_2O\) | \(1.0 \times x^{−14}\) | xiv.00 |
| phosphate ion | \(PO_4^{three−}\) | \(2.1 \times 10^{−ii}\) | 1.68 | \(HPO_4^{2−}\) | \(iv.8 \times 10^{−13}\) | 12.32 |
| dimethylamine | \((CH_3)_2NH\) | \(5.4 \times 10^{−4}\) | three.27 | \((CH_3)_2NH_2^+\) | \(ane.nine \times x^{−11}\) | ten.73 |
| methylamine | \(CH_3NH_2\) | \(4.6 \times 10^{−iv}\) | 3.34 | \(CH_3NH_3^+\) | \(2.ii \times ten^{−11}\) | ten.66 |
| trimethylamine | \((CH_3)_3N\) | \(6.iii \times 10^{−5}\) | iv.xx | \((CH_3)_3NH^+\) | \(1.6 \times ten^{−10}\) | 9.80 |
| ammonia | \(NH_3\) | \(1.8 \times x^{−5}\) | 4.75 | \(NH_4^+\) | \(5.6 \times 10^{−ten}\) | 9.25 |
| pyridine | \(C_5H_5N\) | \(ane.7 \times x^{−9}\) | viii.77 | \(C_5H_5NH^+\) | \(5.9 \times 10^{−6}\) | 5.23 |
| aniline | \(C_6H_5NH_2\) | \(7.4 \times 10^{−10}\) | 9.13 | \(C_6H_5NH_3^+\) | \(1.three \times 10^{−5}\) | 4.87 |
| water | \(H_2O\) | \(1.0 \times 10^{−14}\) | 14.00 | \(H_3O^+\) | \(ane.0^*\) | 0.00 |
At that place is a simple human relationship between the magnitude of \(K_a\) for an acid and \(K_b\) for its cohabit base. Consider, for example, the ionization of hydrocyanic acrid (\(HCN\)) in water to produce an acidic solution, and the reaction of \(CN^−\) with water to produce a bones solution:
\[HCN_{(aq)} \rightleftharpoons H^+_{(aq)}+CN^−_{(aq)} \label{16.5.6} \]
\[CN^−_{(aq)}+H_2O_{(50)} \rightleftharpoons OH^−_{(aq)}+HCN_{(aq)} \label{sixteen.5.7} \]
The equilibrium constant expression for the ionization of HCN is as follows:
\[K_a=\dfrac{[H^+][CN^−]}{[HCN]} \characterization{16.5.8} \]
The corresponding expression for the reaction of cyanide with water is equally follows:
\[K_b=\dfrac{[OH^−][HCN]}{[CN^−]} \label{sixteen.5.9} \]
If nosotros add Equations \(\ref{16.5.6}\) and \(\ref{sixteen.5.7}\), we obtain the post-obit:
| Reaction | Equilibrium Constants |
|---|---|
| \(\abolish{HCN_{(aq)}} \rightleftharpoons H^+_{(aq)}+\abolish{CN^−_{(aq)}} \) | \(K_a=[H^+]\abolish{[CN^−]}/\abolish{[HCN]}\) |
| \(\abolish{CN^−_{(aq)}}+H_2O_{(l)} \rightleftharpoons OH^−_{(aq)}+\cancel{HCN_{(aq)}}\) | \(K_b=[OH^−]\cancel{[HCN]}/\abolish{[CN^−]}\) |
| \(H_2O_{(l)} \rightleftharpoons H^+_{(aq)}+OH^−_{(aq)}\) | \(Thousand=K_a \times K_b=[H^+][OH^−]\) |
In this example, the sum of the reactions described by \(K_a\) and \(K_b\) is the equation for the autoionization of water, and the production of the two equilibrium constants is \(K_w\):
\[K_aK_b = K_w \label{16.5.ten} \]
Thus if nosotros know either \(K_a\) for an acid or \(K_b\) for its cohabit base of operations, we can summate the other equilibrium constant for any conjugate acrid–base of operations pair.
Merely as with \(pH\), \(pOH\), and pKw, we can apply negative logarithms to avoid exponential notation in writing acid and base ionization constants, by defining \(pK_a\) as follows:
\[pKa = −\log_{x}K_a \characterization{xvi.v.11} \]
\[K_a=10^{−pK_a} \label{16.5.12} \]
and \(pK_b\) equally
\[pK_b = −\log_{10}K_b \label{16.five.13} \]
\[K_b=10^{−pK_b} \label{16.5.fourteen} \]
Similarly, Equation \(\ref{16.5.10}\), which expresses the relationship between \(K_a\) and \(K_b\), can exist written in logarithmic form as follows:
\[pK_a + pK_b = pK_w \characterization{16.five.15} \]
At 25 °C, this becomes
\[pK_a + pK_b = 14.00 \label{sixteen.five.sixteen} \]
The values of \(pK_a\) and \(pK_b\) are given for several common acids and bases in Tables \(\PageIndex{1}\) and \(\PageIndex{2}\), respectively, and a more extensive fix of data is provided in Tables E1 and E2. Because of the use of negative logarithms, smaller values of \(pK_a\) represent to larger acid ionization constants and hence stronger acids. For example, nitrous acid (\(HNO_2\)), with a \(pK_a\) of 3.25, is about a million times stronger acid than hydrocyanic acid (HCN), with a \(pK_a\) of 9.21. Conversely, smaller values of \(pK_b\) represent to larger base ionization constants and hence stronger bases.
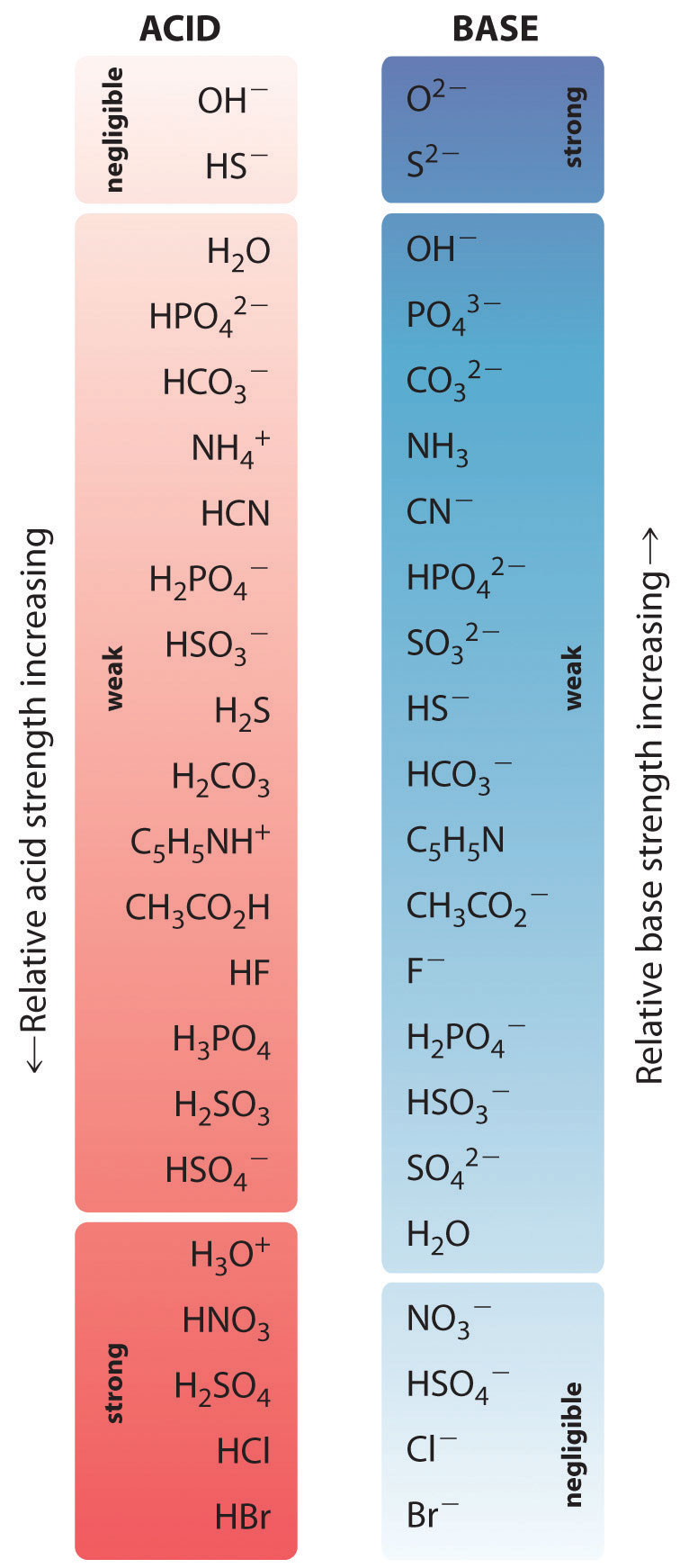
The relative strengths of some common acids and their conjugate bases are shown graphically in Figure \(\PageIndex{1}\). The cohabit acid–base pairs are listed in gild (from top to lesser) of increasing acrid strength, which corresponds to decreasing values of \(pK_a\). This order corresponds to decreasing strength of the conjugate base or increasing values of \(pK_b\). At the bottom left of Figure \(\PageIndex{ii}\) are the common strong acids; at the superlative right are the nigh common potent bases. Notice the inverse relationship between the strength of the parent acid and the strength of the conjugate base. Thus the conjugate base of operations of a strong acid is a very weak base, and the conjugate base of a very weak acid is a strong base.
The cohabit base of a potent acid is a weak base and vice versa.
We tin apply the relative strengths of acids and bases to predict the direction of an acid–base reaction by post-obit a single rule: an acid–base equilibrium always favors the side with the weaker acid and base, every bit indicated past these arrows:
\[\text{stronger acid + stronger base of operations} \ce{ <=>>} \text{weaker acrid + weaker base} \nonumber \]
In an acid–base reaction, the proton always reacts with the stronger base.
For instance, hydrochloric acrid is a strong acrid that ionizes substantially completely in dilute aqueous solution to produce \(H_3O^+\) and \(Cl^−\); only negligible amounts of \(HCl\) molecules remain undissociated. Hence the ionization equilibrium lies nearly all the way to the right, as represented past a unmarried arrow:
\[HCl_{(aq)} + H_2O_{(l)} \rightarrow H_3O^+_{(aq)}+Cl^−_{(aq)} \label{16.5.17} \]
In dissimilarity, acerb acrid is a weak acid, and h2o is a weak base of operations. Consequently, aqueous solutions of acetic acid contain mostly acetic acid molecules in equilibrium with a small concentration of \(H_3O^+\) and acetate ions, and the ionization equilibrium lies far to the left, as represented past these arrows:
\[ \ce{ CH_3CO_2H_{(aq)} + H_2O_{(fifty)} <<=> H_3O^+_{(aq)} + CH_3CO_{2(aq)}^- } \nonumber \]
Similarly, in the reaction of ammonia with water, the hydroxide ion is a strong base, and ammonia is a weak base, whereas the ammonium ion is a stronger acid than water. Hence this equilibrium also lies to the left:
\[H_2O_{(fifty)} + NH_{3(aq)} \ce{ <<=>} NH^+_{4(aq)} + OH^-_{(aq)} \nonumber \]
All acid–base equilibria favor the side with the weaker acid and base. Thus the proton is bound to the stronger base.
- Calculate \(K_b\) and \(pK_b\) of the butyrate ion (\(CH_3CH_2CH_2CO_2^−\)). The \(pK_a\) of butyric acid at 25°C is 4.83. Butyric acid is responsible for the foul smell of rancid butter.
- Calculate \(K_a\) and \(pK_a\) of the dimethylammonium ion (\((CH_3)_2NH_2^+\)). The base ionization constant \(K_b\) of dimethylamine (\((CH_3)_2NH\)) is \(5.4 \times 10^{−4}\) at 25°C.
Given: \(pK_a\) and \(K_b\)
Asked for: corresponding \(K_b\) and \(pK_b\), \(K_a\) and \(pK_a\)
Strategy:
The constants \(K_a\) and \(K_b\) are related as shown in Equation \(\ref{sixteen.5.x}\). The \(pK_a\) and \(pK_b\) for an acid and its conjugate base of operations are related every bit shown in Equations \(\ref{16.five.15}\) and \(\ref{16.5.16}\). Use the relationships pK = −log K and K = 10−pK (Equations \(\ref{xvi.5.11}\) and \(\ref{16.5.thirteen}\)) to catechumen between \(K_a\) and \(pK_a\) or \(K_b\) and \(pK_b\).
Solution:
We are given the \(pK_a\) for butyric acid and asked to calculate the \(K_b\) and the \(pK_b\) for its cohabit base, the butyrate ion. Because the \(pK_a\) value cited is for a temperature of 25°C, we can use Equation \(\ref{sixteen.v.16}\): \(pK_a\) + \(pK_b\) = pKdue west = 14.00. Substituting the \(pK_a\) and solving for the \(pK_b\),
\[4.83+pK_b=14.00 \nonumber \]
\[pK_b=fourteen.00−four.83=9.17 \nonumber \]
Because \(pK_b = −\log K_b\), \(K_b\) is \(10^{−9.17} = half dozen.8 \times ten^{−10}\).
In this case, nosotros are given \(K_b\) for a base (dimethylamine) and asked to calculate \(K_a\) and \(pK_a\) for its conjugate acrid, the dimethylammonium ion. Considering the initial quantity given is \(K_b\) rather than \(pK_b\), we can utilise Equation \(\ref{16.5.ten}\): \(K_aK_b = K_w\). Substituting the values of \(K_b\) and \(K_w\) at 25°C and solving for \(K_a\),
\[K_a(5.4 \times 10^{−iv})=1.01 \times 10^{−14} \nonumber \]
\[K_a=one.9 \times 10^{−11} \nonumber \]
Considering \(pK_a\) = −log \(K_a\), we have \(pK_a = −\log(ane.9 \times 10^{−eleven}) = x.72\). We could also have converted \(K_b\) to \(pK_b\) to obtain the same answer:
\[pK_b=−\log(5.4 \times ten^{−4})=3.27 \nonumber \]
\[pKa+pK_b=fourteen.00 \nonumber \]
\[pK_a=10.73 \nonumber \]
\[K_a=10^{−pK_a}=ten^{−10.73}=one.nine \times x^{−11} \nonumber \]
If we are given any i of these 4 quantities for an acid or a base (\(K_a\), \(pK_a\), \(K_b\), or \(pK_b\)), we tin can calculate the other three.
Lactic acid (\(CH_3CH(OH)CO_2H\)) is responsible for the pungent taste and smell of sour milk; it is besides thought to produce soreness in fatigued muscles. Its \(pK_a\) is 3.86 at 25°C. Summate \(K_a\) for lactic acid and \(pK_b\) and \(K_b\) for the lactate ion.
- Respond
-
- \(K_a = ane.4 \times ten^{−iv}\) for lactic acid;
- \(pK_b\) = ten.14 and
- \(K_b = 7.ii \times ten^{−11}\) for the lactate ion
A Video Computing pH in Stiff Acrid or Strong Base Solutions: Calculating pH in Strong Acid or Strong Base of operations Solutions [youtu.be]
Solutions of Strong Acids and Bases: The Leveling Effect
You will notice in Table \(\PageIndex{1}\) that acids like \(H_2SO_4\) and \(HNO_3\) lie in a higher place the hydronium ion, pregnant that they have \(pK_a\) values less than zip and are stronger acids than the \(H_3O^+\) ion. Call back from Affiliate four that the acidic proton in virtually all oxoacids is bonded to 1 of the oxygen atoms of the oxoanion. Thus nitric acrid should properly exist written as \(HONO_2\). Unfortunately, however, the formulas of oxoacids are about always written with hydrogen on the left and oxygen on the right, giving \(HNO_3\) instead. In fact, all six of the common stiff acids that we first encountered in Chapter 4 accept \(pK_a\) values less than cipher, which means that they take a greater tendency to lose a proton than does the \(H_3O^+\) ion. Conversely, the conjugate bases of these strong acids are weaker bases than water. Consequently, the proton-transfer equilibria for these strong acids lie far to the right, and adding whatever of the mutual strong acids to water results in an essentially stoichiometric reaction of the acid with h2o to grade a solution of the \(H_3O^+\) ion and the cohabit base of the acrid.
Although \(K_a\) for \(HI\) is about 108 greater than \(K_a\) for \(HNO_3\), the reaction of either \(Hi\) or \(HNO_3\) with water gives an essentially stoichiometric solution of \(H_3O^+\) and I− or \(NO_3^−\). In fact, a 0.1 M aqueous solution of whatever stiff acrid actually contains 0.i Thousand \(H_3O^+\), regardless of the identity of the strong acid. This phenomenon is called the leveling consequence: any species that is a stronger acrid than the conjugate acid of h2o (\(H_3O^+\)) is leveled to the strength of \(H_3O^+\) in aqueous solution considering \(H_3O^+\) is the strongest acid that tin be in equilibrium with h2o. Consequently, information technology is incommunicable to distinguish betwixt the strengths of acids such as HI and HNO3 in aqueous solution, and an culling approach must exist used to determine their relative acid strengths.
Ane method is to use a solvent such as anhydrous acerb acid. Because acetic acrid is a stronger acid than water, it must as well be a weaker base, with a bottom trend to have a proton than \(H_2O\). Measurements of the conductivity of 0.1 M solutions of both HI and \(HNO_3\) in acetic acid evidence that Hullo is completely dissociated, but \(HNO_3\) is just partially dissociated and behaves like a weak acid in this solvent. This effect clearly tells u.s. that HI is a stronger acid than \(HNO_3\). The relative order of acid strengths and approximate \(K_a\) and \(pK_a\) values for the stiff acids at the top of Tabular array \(\PageIndex{1}\) were adamant using measurements like this and dissimilar nonaqueous solvents.
In aqueous solutions, \(H_3O^+\) is the strongest acid and \(OH^−\) is the strongest base that can be in equilibrium with \(H_2O\).
The leveling effect applies to solutions of stiff bases likewise: In aqueous solution, any base of operations stronger than OH− is leveled to the strength of OH− considering OH− is the strongest base of operations that can exist in equilibrium with water. Salts such equally \(K_2O\), \(NaOCH_3\) (sodium methoxide), and \(NaNH_2\) (sodamide, or sodium amide), whose anions are the conjugate bases of species that would lie beneath water in Tabular array \(\PageIndex{2}\), are all stiff bases that react essentially completely (and oftentimes violently) with water, accepting a proton to give a solution of \(OH^−\) and the respective cation:
\[K_2O_{(s)}+H_2O_{(l)} \rightarrow 2OH^−_{(aq)}+2K^+_{(aq)} \label{xvi.5.xviii} \]
\[NaOCH_{three(s)}+H_2O_{(l)} \rightarrow OH^−_{(aq)}+Na^+_{(aq)}+CH_3OH_{(aq)} \characterization{sixteen.5.nineteen} \]
\[NaNH_{2(s)}+H_2O_{(l)} \rightarrow OH^−_{(aq)}+Na^+_{(aq)}+NH_{3(aq)} \label{16.v.20} \]
Other examples that you may encounter are potassium hydride (\(KH\)) and organometallic compounds such equally methyl lithium (\(CH_3Li\)).
Polyprotic Acids and Bases
As y'all learned, polyprotic acids such as \(H_2SO_4\), \(H_3PO_4\), and \(H_2CO_3\) contain more one ionizable proton, and the protons are lost in a stepwise manner. The fully protonated species is always the strongest acrid considering it is easier to remove a proton from a neutral molecule than from a negatively charged ion. Thus acid strength decreases with the loss of subsequent protons, and, correspondingly, the \(pK_a\) increases. Consider \(H_2SO_4\), for example:
\[HSO^−_{4 (aq)} \ce{ <=>>} And then^{ii−}_{4(aq)}+H^+_{(aq)} \;\;\; pK_a=-2 \nonumber \]
The equilibrium in the first reaction lies far to the right, consistent with \(H_2SO_4\) being a strong acid. In contrast, in the 2d reaction, observable quantities of both \(HSO_4^−\) and \(SO_4^{2−}\) are present at equilibrium.
For a polyprotic acid, acrid force decreases and the \(pK_a\) increases with the sequential loss of each proton.
The hydrogen sulfate ion (\(HSO_4^−\)) is both the conjugate base of \(H_2SO_4\) and the conjugate acid of \(SO_4^{two−}\). Just like water, HSO4− can therefore act equally either an acid or a base, depending on whether the other reactant is a stronger acid or a stronger base. Conversely, the sulfate ion (\(SO_4^{ii−}\)) is a polyprotic base that is capable of accepting 2 protons in a stepwise mode:
\[Then^{2−}_{iv (aq)} + H_2O_{(aq)} \ce{ <=>>} HSO^{−}_{four(aq)}+OH_{(aq)}^- \nonumber \]
\[HSO^{−}_{4 (aq)} + H_2O_{(aq)} \ce{ <=>>} H_2SO_{iv(aq)}+OH_{(aq)}^- \label{sixteen.6} \]
Like any other conjugate acid–base pair, the strengths of the cohabit acids and bases are related past \(pK_a\) + \(pK_b\) = pKw. Consider, for example, the \(HSO_4^−/ SO_4^{2−}\) conjugate acid–base of operations pair. From Table \(\PageIndex{1}\), we run across that the \(pK_a\) of \(HSO_4^−\) is 1.99. Hence the \(pK_b\) of \(SO_4^{2−}\) is fourteen.00 − 1.99 = 12.01. Thus sulfate is a rather weak base, whereas \(OH^−\) is a strong base of operations, so the equilibrium shown in Equation \(\ref{16.half dozen}\) lies to the left. The \(HSO_4^−\) ion is also a very weak base (\(pK_a\) of \(H_2SO_4\) = 2.0, \(pK_b\) of \(HSO_4^− = 14 − (−2.0) = 16\)), which is consequent with what we expect for the cohabit base of a stiff acid.
Predict whether the equilibrium for each reaction lies to the left or the right as written.
- \(NH^+_{4(aq)}+PO^{iii−}_{iv(aq)} \rightleftharpoons NH_{3(aq)}+HPO^{2−}_{iv(aq)}\)
- \(CH_3CH_2CO_2H_{(aq)}+CN^−_{(aq)} \rightleftharpoons CH_3CH_2CO^−_{2(aq)}+HCN_{(aq)}\)
Given: balanced chemical equation
Asked for: equilibrium position
Strategy:
Identify the cohabit acrid–base of operations pairs in each reaction. Then refer to Tables \(\PageIndex{1}\)and\(\PageIndex{two}\) and Figure \(\PageIndex{2}\) to determine which is the stronger acid and base. Equilibrium always favors the formation of the weaker acid–base pair.
Solution:
The cohabit acid–base pairs are \(NH_4^+/NH_3\) and \(HPO_4^{ii−}/PO_4^{3−}\). According to Tables \(\PageIndex{one}\) and \(\PageIndex{ii}\), \(NH_4^+\) is a stronger acrid (\(pK_a = 9.25\)) than \(HPO_4^{2−}\) (pKa = 12.32), and \(PO_4^{3−}\) is a stronger base (\(pK_b = i.68\)) than \(NH_3\) (\(pK_b = iv.75\)). The equilibrium will therefore lie to the right, favoring the formation of the weaker acrid–base pair:
\[ \underset{\text{stronger acid}}{NH^+_{iv(aq)}} + \underset{\text{stronger base}}{PO^{3-}_{4(aq)}} \ce{<=>>} \underset{\text{weaker base}}{NH_{3(aq)}} +\underset{\text{weaker acid}} {HPO^{2-}_{4(aq)}} \nonumber \]
The conjugate acrid–base pairs are \(CH_3CH_2CO_2H/CH_3CH_2CO_2^−\) and \(HCN/CN^−\). According to Tabular array \(\PageIndex{1}\), HCN is a weak acrid (pKa = 9.21) and \(CN^−\) is a moderately weak base (pKb = 4.79). Propionic acid (\(CH_3CH_2CO_2H\)) is not listed in Table \(\PageIndex{1}\), notwithstanding. In a situation like this, the all-time approach is to look for a like compound whose acid–base backdrop are listed. For case, propionic acrid and acerb acrid are identical except for the groups fastened to the carbon atom of the carboxylic acid (\(\ce{−CH_2CH_3}\) versus \(\ce{−CH_3}\)), and so nosotros might look the two compounds to have like acid–base of operations backdrop. In particular, nosotros would expect the \(pK_a\) of propionic acrid to be like in magnitude to the \(pK_a\) of acetic acrid. (In fact, the \(pK_a\) of propionic acid is 4.87, compared to 4.76 for acetic acid, which makes propionic acid a slightly weaker acid than acetic acrid.) Thus propionic acrid should exist a significantly stronger acid than \(HCN\). Because the stronger acid forms the weaker conjugate base, we predict that cyanide will be a stronger base of operations than propionate. The equilibrium volition therefore lie to the correct, favoring the germination of the weaker acid–base pair:
\[ \underset{\text{stronger acid}}{CH_3CH_2CO_2H_{(aq)}} + \underset{\text{stronger base}}{CN^-_{(aq)}} \ce{<=>>} \underset{\text{weaker base}}{CH_3CH_2CO^-_{2(aq)}} +\underset{\text{weaker acid}} {HCN_{(aq)}} \nonumber \]
Predict whether the equilibrium for each reaction lies to the left or the right as written.
- \(H_2O_{(l)}+HS^−_{(aq)} \rightleftharpoons OH^−_{(aq)}+H_2S_{(aq)}\)
- \(HCO^−_{two(aq)}+HSO^−_{4(aq)} \rightleftharpoons HCO_2H_{(aq)}+And so^{ii−}_{4(aq)}\)
- Answer a
-
left
- Answer b
-
left
A Video Discussing Polyprotic Acids: Polyprotic Acids [youtu.exist]
Summary
Acid–base reactions e'er contain ii conjugate acrid–base pairs. Each acid and each base has an associated ionization abiding that corresponds to its acrid or base strength. Two species that differ past just a proton constitute a cohabit acid–base of operations pair. The magnitude of the equilibrium constant for an ionization reaction can be used to make up one's mind the relative strengths of acids and bases. For an aqueous solution of a weak acid, the dissociation constant is called the acid ionization constant (\(K_a\)). Similarly, the equilibrium constant for the reaction of a weak base of operations with water is the base ionization constant (\(K_b\)). For whatsoever conjugate acrid–base pair, \(K_aK_b = K_w\). Smaller values of \(pK_a\) correspond to larger acid ionization constants and hence stronger acids. Conversely, smaller values of \(pK_b\) represent to larger base ionization constants and hence stronger bases. At 25°C, \(pK_a + pK_b = 14.00\). Acid–base reactions always go on in the direction that produces the weaker acid–base pair. No acid stronger than \(H_3O^+\) and no base stronger than \(OH^−\) can exist in aqueous solution, leading to the phenomenon known as the leveling effect. Polyprotic acids (and bases) lose (and gain) protons in a stepwise manner, with the fully protonated species beingness the strongest acrid and the fully deprotonated species the strongest base.
Key Equations
- Acid ionization constant: \[K_a=\dfrac{[H_3O^+][A^−]}{[HA]} \nonumber \]
- Base ionization abiding: \[K_b= \dfrac{[BH^+][OH^−]}{[B]} \nonumber \]
- Human relationship between \(K_a\) and \(K_b\) of a conjugate acid–base of operations pair: \[K_aK_b = K_w \nonumber \]
- Definition of \(pK_a\): \[pKa = −\log_{ten}K_a \nonumber \] \[K_a=10^{−pK_a} \nonumber \]
- Definition of \(pK_b\): \[pK_b = −\log_{ten}K_b \nonumber \] \[K_b=x^{−pK_b} \nonumber \]
- Relationship between \(pK_a\) and \(pK_b\) of a cohabit acrid–base of operations pair: \[pK_a + pK_b = pK_w \nonumber \] \[pK_a + pK_b = xiv.00 \; \text{at 25°C} \nonumber \]
Ka Expression For Acetic Acid,
Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_A_Molecular_Approach_(Tro)/16%3A_Acids_and_Bases/16.04%3A_Acid_Strength_and_the_Acid_Dissociation_Constant_(Ka)
Posted by: campbellwathre.blogspot.com


0 Response to "Ka Expression For Acetic Acid"
Post a Comment